限制邏輯是一種非單調邏輯,通常簡稱限制,是模卡斯 (mecarth,j.) 於 1980 年提出的一種有代表性的非單調推理理論。
基本介紹
- 中文名:限制
- 外文名:circumscription
- 適用範圍:數理科學
簡介,限制公理,套用,
簡介
限制通常指(circumscription),這是一種非單調邏輯,是模卡斯 (mecarth,j.) 於 1980 年提出的一種有代表性的非單調推理理論。
限制是在一個低階公式(一階公式)a 的所有 p 極小(化)模型中都為真的一個較高階公式(二階公式),這裡 p 是 a 中相對於一定準則的極小變數,直觀上,限制的基本思想是捕捉一種猜測推理的經濟原則,即從某些事實 a 出發能夠推出具有某一性質 p 的對象就是滿足 p 的全部對象。
令 a(p,x) 是一個包含謂詞 p 與變元 x 的一階句子,語義上,a 中限制 p,是相對於一個偏序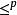 的所有 p 極小模型都為真的句子集,一個 a 的模型 m 稱為極小的,若不存在它的其他模型 m‘ 使得
的所有 p 極小模型都為真的句子集,一個 a 的模型 m 稱為極小的,若不存在它的其他模型 m‘ 使得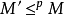 ,定義
,定義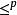 如下:令
如下:令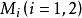 ,是兩個模型,
,是兩個模型,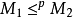 ,若且唯若:
,若且唯若:
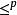
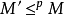
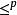
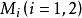
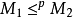
(1) m1與m2具有相同的論域;
(2) p 在 m1 的外延包含於 p 在 m2 的外延,語法上,限制可刻畫如下二階句子:
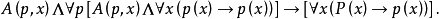
限制公理
限制公理亦稱公理、正則公理 (axiom of regularity) ,是集合論的一條重要公理。
任何非空集合都有 極小元素,這個公理形式化為:
極小元素,這個公理形式化為: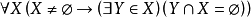 或
或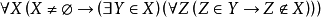 。該公理斷言:任何集合在關係
。該公理斷言:任何集合在關係 下是良基的,不存在無限遞降鏈
下是良基的,不存在無限遞降鏈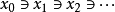 也就不會有
也就不會有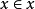 與循環
與循環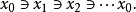 實質上此公理是對集合概念的一種限制:有性質
實質上此公理是對集合概念的一種限制:有性質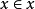 的集合是不存在的。
的集合是不存在的。

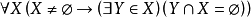
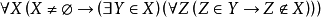

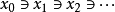
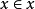
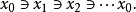
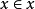
該公理的另一表述方法是:對任何集合論公式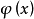 ,有
,有
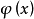
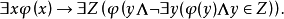
套用
限制存在許多變體,例如可限制謂詞元組而且允許某些謂詞合函式變化,它們具有不同的表達能力,一般地,限制具有可靠性定理,但沒有一般的完全性成果,由於限制是二階形式,計算上比較困難,這也是非單調邏輯的共性問題,由於限制是一階邏輯的直接擴充,具有一階邏輯於極小模型的良好性質,因此限制是非單調邏輯中的代表作,對它已有充分的研究和廣泛的套用。

