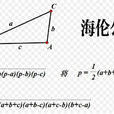
海倫公式又譯作希倫公式、海龍公式、希羅公式、海倫－秦九韶公式。它是利用三角形的三條邊的邊長直接求三角形面積的公式。表達式為：，它的特點是形式漂亮，便於記憶。
相傳這個公式最早是由古希臘數學家阿基米德得出的，而因為這個公式最早出現在海倫的著作《測地術》中，所以被稱為海倫公式。中國秦九韶也得出了類似的公式，稱三斜求積術。
基本介紹
- 中文名：海倫公式
- 外文名：heron's formula
- 別稱：
- 表達式：s=√p(p-a)(p-b)(p-c)
- 提出者：
- 套用學科：數學幾何
- 適用領域範圍：三角計算
公式表述,驗證推導,勾股定理,恆等式,其它證明,推廣拓展,發展簡史,公式意義,
公式表述
海倫公式：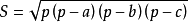
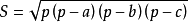
假設在平面內，有一個三角形，邊長分別為a、b、c，三角形的面積s可由以下公式求得：
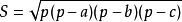
而公式里的p為半周長（周長的一半）：
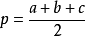
注1："metrica"《度量論》手抄本中用s作為半周長，所以
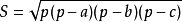
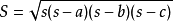
它的特點是形式漂亮，便於記憶。
驗證推導
勾股定理
證明：如右圖，
，根據勾股定理，得：
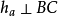
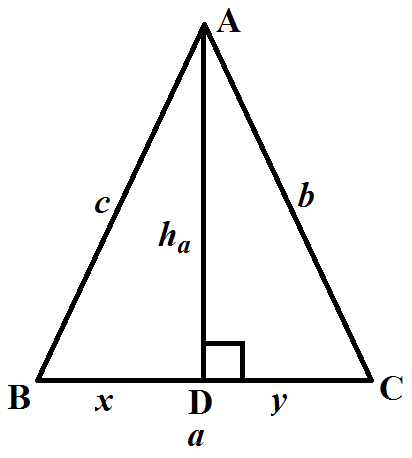
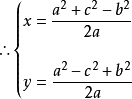
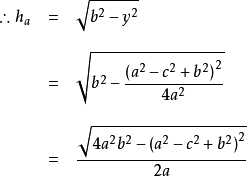
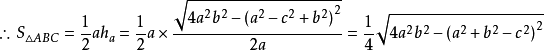
此時化簡得出海倫公式，證畢。
恆等式
證明：若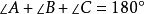
，則
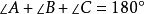
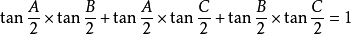
證明，如圖：
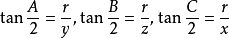
根據恆等式，得：
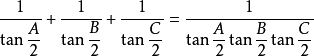
將上面代入，得：
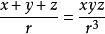
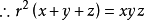
如圖可知：
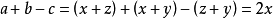
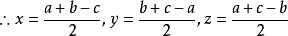
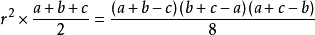
兩邊同乘以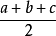
，得：
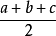
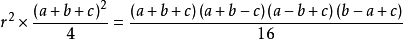
兩邊開方得出海倫公式，證畢。
其它證明
推廣拓展
一般來講僅用四邊長無法表達某個四邊形面積（某些特例除外），必須添加某些條件，比如角、對角線等。
(brahmagupta)在公元7世紀初的一部論及天文的著作中，給出了用四邊長a、b、c、d表達圓內接四邊形面積的：
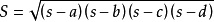
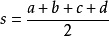
公式無論從形式上還是內容上都是海倫公式的延拓與推廣，但它僅適用於圓內接四邊形。當然，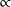
為四邊形對角和之半時，依然有公式：
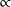
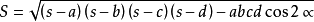
由於任何n邊的多邊形都可以分割成（n-2）個三角形，所以海倫公式可以用作求多邊形面積的公式，但需要先知道分割用的對角線的長度。
發展簡史
古希臘的數學發展到里亞時期，數學的套用得到了很大的發展，其突出的一點就是三角術的發展，在解三角形的過程中，其中一個比較難的問題是如何利用三角形的三邊直接求出三角形面積。
阿基米德
阿基米德這個公式是由古希臘數學家得出的，但人們常常以古希臘的數學家命名這個公式，稱此公式為海倫公式，因為這個公式最早出現在海里的著作《測地術》中，並在海倫的著作《測量儀器》和《度量數》中給出證明。
中國宋代的數學家秦九韶在1247年獨立提出了“”，雖然它與海倫公式形式上有所不同，但它完全與海倫公式等價，它填補了中國數學史中的一個空白，從中可以看出中國古代已經具有很高的數學水平。
公式意義
海倫公式的提出為三角形和多邊形的面積計算提供了新的方法和思路，在知道三角形三邊的長而不知道高的情況下使用海倫公式可以更快更簡便的求出面積，比如說在測量土地的面積的時候，不用測，只需測兩點間的距離，就可以方便地導出答案。
